我在为平博撰写的上一篇文章中探讨了破产这一主题，并探究了不同类型的博彩玩家在不同情境中遭遇破产的可能性。人工智能领域专家和WinnerOdds网站所有人Miguel Figueres在他的电子书《如何打败博彩公司》中提出了非常相似的观点：“博彩玩家极少等到[破产]才改变[自己的]方法或停止博彩。”

恰恰相反，他们通常会在破产可能性冒头之前早早改变策略或者彻底抽身。这种情况具体会在哪个时间点上发生极大地取决于博彩玩家对待风险的态度，不过找到对之加以定义和建模的方法很有用处。回撤和最大回撤（MDD）是金融投资界人士非常熟悉的两个概念。我将在本文中解释它们的定义、预期及应对方法。

什么是回撤和最大回撤？

Investopedia网站将回撤和最大回撤分别定义为“某一特定投资记录时期内，最高值回落至最低值（百分比）的幅度”以及“在达到新的峰值之前，最高值回落至最低值（百分比）的最大幅度”。博彩玩家的盈利史和金融投资的演化类型基本一致，因此这些概念完全可以照搬到博彩界。

我们还可以合理地将最大回撤视为博彩玩家实际能够忍受的最大总资金回落。Miguel在他的电子书中将这一数值定为50%，然而这个数字完全是主观得出的。因此，如果我们能就最大回撤预期进行建模，帮助我们对自己的博彩体验进行风险管理，那将大有裨益。

影响最大回撤的因素

Miguel指出了数个影响最大回撤（MDD）大小的因素。不出所料，预期利润（以及收益）越大，预期MDD就越小。类似的是，在其他条件都相同的情况下，投注在更高赔率上的博彩玩家会遭遇更大的变化，面临着更大的资金波动风险，因此也有更大的预期MDD。

Miguel还解释道，随着投注数量的增加，预期MDD呈对数增长。例如，在一个简单的50-50二元投注中，投下2n个投注的预期最长损失时长大约等于n。

建模预期最大回撤

按照Miguel的逻辑，我进行了一定数量的蒙特卡罗模拟，试图建立不同的博彩玩家进行一系列1,000个等额本金（1个单位）投注的预期MDD（以单位计算）模型。五个不同的赔率（1.5、2、3、5和10）各假设有2%到20%（间隔为2%）的预期收益，即总共有50种不同的情境。每种情境都进行了10,000次迭代。下表中总结了预期（平均）MDD。

建模预期最大回撤

假设有这样一位典型的十分敏锐的让分盘博彩玩家，他投注的赔率大约为2。如果成功率为53%，这些投注的收益率大约为6%。在进行一系列1,000个投注之后，预期最大回撤大约较上一峰值回落22个单位。

导致不一致性和不理想表现的最大原因是决策受到了情绪的干扰。

相比之下，假设有一位典型的技巧娴熟的赛马博彩玩家，他投注的平均赔率约为5，收益率为14%；MDD几乎翻倍（43个单位）。如果在更高的赔率上表现得更差，那么预期MDD可能超过100个单位。在初始资金是100个单位的情况下，个中影响不言而喻。

当然，正如我在之前那篇文章中提到的那样，比起喜欢投注更低赔率的博彩玩家，承受更高赔率投注带来的更大变化的博彩玩家通常会降低本金大小，因而减少了MDD的绝对值大小。

上表中的数值应该能够帮助博彩玩家判定出合适的投注本金大小。例如，如果将本金减小到0.25个单位，从赔率10上得到4%收益率的博彩玩家的MDD将从100个降到25个单位。在这种情况下，哪怕初始资金只有100个单位，影响也没有那么难以让人接受。 

最大回撤概率分布

当然，从上表中我们可以知道平均MDD预期。但是我们无法从中预知，MDD如何随着我们运气的好坏变化而变化。对此，我们需要制定概率分布图。下方第一张图表中显示了赔率为2的10种情境的概率分布。

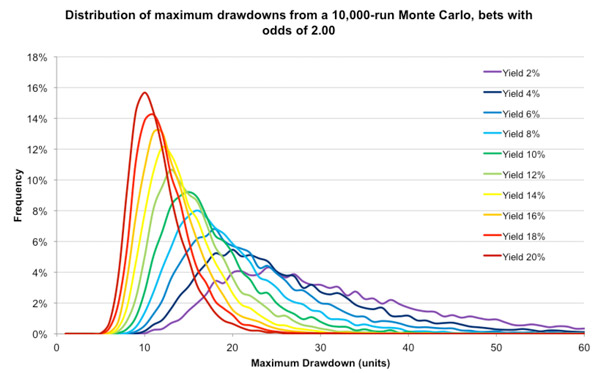
每种情境的概率分布都呈正偏态，更长的右侧尾部代表着某些MDD可能非常高。因此，每种情景的平均或预期MDD都会大于中位数和众数。（众数即出现次数最多的MDD对应每个分布的高点。）读者们可以忽略曲线中的不完美；如果进行更大数量的蒙特卡罗迭代（这超出了我的计算处理能力）的话，这些不完美就会消失。

假设收益率为6%。最常见的MDD为18个单位。然而平均值为22个单位。在我的10,000次迭代中，几乎有三分之一的最大回撤为25个或更多个单位，最高达73个单位。平均值能给我们提供很多信息，但是概率分布的形状给了我们更多有用的信息，让我们了解好运和坏运情境中的预期范围。

第二张图表显示收益率为10%的不同赔率的五个模型情境。可能结果的分布变化巨大。例如，当投注赔率为10时，尽管预期MDD是84个单位，但是四分之一的蒙特卡罗迭代都达到了100个或更多个单位，其中一个甚至高达302个单位。

如果你是在高赔率上投注的娴熟博彩玩家，那么当你的资金为100个单位时，像这样的1/10,000的可能性必然要你将本金变为0.1个单位，才能让MDD的大小降到可以承受的范围。

回撤心理学

没人喜欢在博彩上输钱；这一点无需赘言。但是现实比这要残酷的多。要弥补之前的损失，就要有更大百分比的增长，因为回撤会摧毁你的资金，而这些资金在你赢钱的情况下本来能帮你盈利。这个问题是指数级的。

10%的回撤需要11%的增长来弥补。但是50%的回撤却需要100%的增长才能弥补，而75%的回撤更是需要300%的增长。 

如果你能将自己从赢钱输钱的情绪波动中抽离出来，就能更好地坐稳体育博彩这趟过山车。

此外，Daniel Kahneman和Amos Tversky的行为经济学著作已经指出，相对而言，失败带来的苦痛远远超过胜利带来的喜悦，苦痛的平均强度起码是喜悦的两倍。因此毫不奇怪，虽然当某人的资金增长50%时，人们会对此作出自我肯定的成功解释，但类似的回撤却会让人们质疑使用方法背后的原理，甚至质疑是否应该博彩。

由于没有关于这些结果为何发生的更多信息，我们更容易对其原因作出错误的结论。可以说，成功会让我们对自己的预期能力过度自信，而常常忽视随机性的影响。

另一方面，失败会让我们放弃自己使用的方法，让它们没有机会完全展示自己的真实长期预期。在这里我举一个极端的例子：许多年前，我仅在投下10个投注之后就抛弃了一种投注系统，因为其中8个投注都输了。这，就是损失厌恶的魔力。 

如何管理回撤？

所有盈利博彩玩家早晚都会遭遇这样的时间节点——面对着重大回撤，质疑自己的策略是否有误。他们面对的最大挑战或许是学习如何应对它们。导致不一致性和不理想表现的最大原因是决策受到了情绪的干扰。

职业体育博彩玩家会试图从自己的投注行为中剥离掉情绪。假以时日，博彩玩家应该能变得输赢不惊。当然，剥离情绪需要人们对自己的长期能力有一定程度的自信，还需要支撑这一点的证据。 

要弥补之前的损失，就要有更大百分比的增长，因为回撤会摧毁本来能帮你盈利的资金。

不要做出追回损失这一愚行是博彩的黄金法则之一。然而，赢钱的时候增加投注本金虽然可能没前者那么有毁灭性，但也一样不正确，除非通过某种类型的凯利公式进行合理的资金管理。

上述都是赌徒谬误的例子，它们忽略了利润和损失演变中固有的随机性，即使对于拥有长期盈利预期的博彩玩家也是一样。在我有相关数据的一个博彩史中，博彩玩家在仅仅278个投注后就赚取了4位数的利润，紧接着大幅提高了投注本金，从大约€50提高到了€400。接下来还没投到100个投注，他们赚到的利润就几乎全输光了。

在《博彩的科学、心理学和哲学》的最后，我总结了聪明的博彩玩家应该具备的素质。所有这些素质都有助于博彩玩家从博彩中抽离情绪并学会如何应对回撤。

聪明的博彩玩家会思考概率而非简单地以输赢对错来判断，他们能认识到博彩中发生的大部分事情都是运气使然，个中因果关联微乎其微。他们会抵抗住颠倒因果关系的诱惑；他们不会将结果归功于自己头上，反而会审视自己的预测方法，分析该方法成就输赢的频率。

所有职业博彩玩家都知道，单个投注的输赢几乎或完全不能说明其潜在价值。正好相反，聪明的博彩玩家宁愿输掉有预期价值的投注，也不愿赢得没有预期价值的投注，这也许是最重要的一点。如果你能将自己从赢钱输钱的情绪波动中抽离出来，只关注投注的预期价值，就能更好地坐稳体育博彩这趟过山车。