平博交易总监Marco Blume明确表示过，评估博彩玩家是否拥有长期盈利，意即他们是否精明的一个可靠指标是看他们能否打败收盘赔率。

普遍认为，市场的收盘价格是所有投注赔率中最有效或者说最准确的，因为它所反映出的可用比赛信息量确实最大。如果在受到抽水的影响之后，它反映出某件事情发生的“真实”概率，那么你超出它的任何部分都是衡量你拥有的预期优势的一个指标。

比它高10%，那么你就可以预期自己的长期利润为10%。但是还有一些人认为，尽管打败收盘赔率是娴熟技术的重要标志，然而它却并不一定是先决条件。不过如果这一点是真的，那就意味着收盘赔率并不总是完全有效。

在本文中，我想尝试调和这两种论调。为就此达成共识，我将再次审视效率这一概念，特别是平博收盘赔率的效率。我在这里必须要说，这篇文章是我的一次统计思想实验之旅，可能不适合胆小者。

当我踏上这一旅程时，我并不确定我会发现什么。哪怕到了结束时，我仍旧对结论持不确定态度，但是请和我一同享受这趟旅程。这可能没有造访威利旺卡的巧克力工厂那么有趣，但是我希望它对那些立志成为精明博彩玩家的人有所启迪。 

什么是市场效率？

过去几年里，我就市场效率这个概念做过多番探讨。在博彩环境中，有效市场指的是投注赔率准确反映出所涉事件潜在结果概率的市场。例如，如果曼城战胜同城对手曼联的“真实”概率为70%，那么如果赔率在博彩公司加入抽水之前是1.429的话，那它就是有效的。 

毕竟，博彩市场是个很有效的贝叶斯处理器，它一直在不断地优化、升级并改进对事件发生概率的看法。

当然，就某一场比赛来说，总有一个结果，投在曼城上的投注要么赢，要么输。然而，重复成千上万次之后，单个投注的好运坏运对单场比赛的影响将被抵消（大数法则）。因此，探讨“真实”结果概率仍旧有其意义所在，尽管实际上不可能知道精确的数值。毕竟投注赔率所反映的就是它。

市场效率是个应用于大样本的有趣概念。然而，对于单个事件，如果我们不可能真的知道结果的“真实”概率到底是多少，那么我们怎么能知道投注赔率的效率到底如何？ 

当然我们可以测试数量较大的投注样本，假设公平赔率（不含抽水）为2.00。如果它们中50%都胜利，那么这些投注的总体平均赢率大约是50%，因此平均而言，这些投注合理地反映出了它们的潜在赢率。但是由此我们并不能知道为总体平均值做出贡献的每个投注的赢率。市场总体上来看可能很有效，但在逐个投注的基础上却掩蔽了潜在的低效性。

平博收盘赔率的效率如何？

2016年7月，平博发表了我的文章。那篇文章揭示出他们的足球比赛投注赔率，特别是他们的收盘赔率，即比赛开始前发布的最终价格的有效性（或者说准确性）。

我在文章中指出，移除他们的抽水之后，2.00的赔率拥有大约50%的赢率，3.00的赔率拥有33%的赢率，4.00的赔率拥有25%的赢率，以此类推。当然，正如上文中解释的那样，我们从中完全没办法知道单场比赛的“真实”结果概率，只能知道平均而言，赔率挺准确的。

除此之外，我还阐释了平博开盘收盘价格之比非常可靠地指示出利润率，暗示他们的收盘赔率极为有效。例如，开盘赔率为2.20（移除掉抽水）而收盘赔率降至2.00的球队赢得比赛的概率约为50%，固定金额投注在开盘赔率（或者2.20/2.00-1）上的利润回报为10%，而在收盘赔率上则为0%。

另一方面，开盘赔率为1.80然后升至2.00的球队赢得比赛的概率约为50%，固定金额投注在开盘赔率（1.80/2.00-1）上的损失为10%，而在收盘赔率上则为0%。我使用更大的数据样本（158,092场比赛，474,278个主/平/客投注赔率）再次运行了分析，结果大致相同。具体如下图所示。

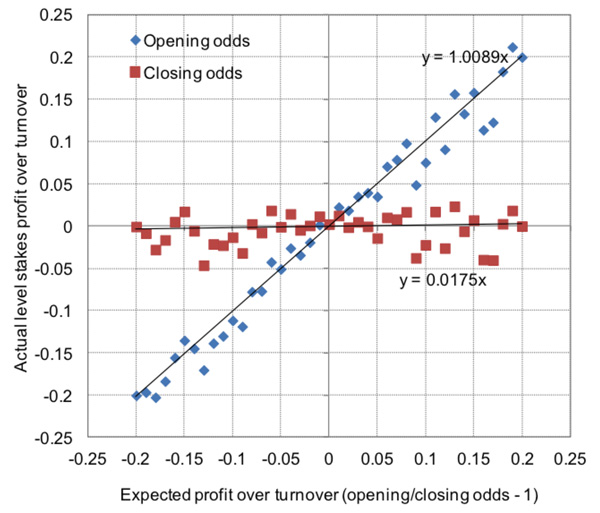
每个数据点代表开盘/收盘赔率之比间隔1%的实际回报。蓝色圆点是开盘赔率回报，红色圆点是收盘赔率回报。显然存在一些潜在的变动性，但大体上的趋势是明确的。我在图中显示出了趋势线——我选择将它们的截距设为零（可以说是移除抽水时的合理假设），图中还显示了它们的方程式。

它们几乎完美地再次确认了我最初的假设，即开盘收盘赔率之比（图中的x）可完美地预示开盘赔率（图中的y）的利润率，以及更广泛地说，平博收盘赔率平均而言极为有效。

开盘/收盘赔率之比（减去1）和利润率（或者说收益）之间的“比例系数”是趋势线的梯度值。如果值为1，就代表完美比例。为简略起见，在本文剩余部分，我将使用英文首字母缩写OCRYCOP来代表该系数。

但是我要再次指出，我们仍旧只知道这只是总体上的“真实”。我们还是不知道单个收盘赔率实际上效率如何。图中的每个数据点都有数千场比赛贡献数据。

为市场效率建模

为了让大家知道我们如何得到这样一个代表收盘赔率效率的OCRYCOP图表，我建立了一个模拟开盘至收盘赔率变动的简易模型。此模型包含10,000个投注，每个都有开盘和收盘赔率。 

为了复制投注“真实”结果概率的不确定性，我决定将开盘赔率随机定为平均2.00左右，（σ）为0.15（也就是说约三分之二在1.85和2.15之间，95％落在1.70和2.30之间）。 

因此，尽管只有拉普拉斯妖（还有我）知道每个投注的“真实”价格为2.00，我的模型中假想出来的博彩公司发布的开盘赔率仍在那个平均值左右变化。我将标准差设为0.15是因为它大致反映出赔率接近2.00的真实投注市场中观察到的开盘至收盘赔率变动情况。

举例来说，0.05的标准差暗示，已公布的大致在2.00的开盘赔率中，95%会精确到±5%之间。考虑到实际观察到的价格变动量，这个范围似乎过窄。同样，0.3或更高的数字表明博彩公司并不擅长设定赔率，我们知道赔率通常并不是“真实”的。 

市场效率是个应用于大样本的有趣概念。然而，对于单个事件，如果我们不可能真的知道结果的“真实”概率到底是多少，那么我们怎么能知道投注赔率的效率到底如何？

博彩公司极不可能对2.00的“真实”赔率设置3.00的价格。当然这种情况确实可能发生，但它通常是个明显的错误或者某些无法预料的重要新闻（他们在设定赔率时没有得到这些消息）导致的结果。当然在这种情况下，谈论“真实”价格的变化也是非常合理的。好了，让我们回到模型中。我已经制定了一些开盘赔率，那么收盘赔率呢？

理论上说，收盘赔率反映的是博彩玩家从经济角度表达出来的看法。让我们假设在极端情况下，尽管这些观点反映出了关于“真实”结果概率的信息积累，但仍存在相同水平的固有随机不确定性。显然这并不现实——毕竟，博彩市场是个很有效的贝叶斯处理器，它一直在不断地优化、升级并改进对事件发生概率的看法，从而降低与此相关的不确定性。

我们的模型中使用的平均价格和标准差再一次分别是2.00和0.15。我们现在可以计算出每对开盘和收盘赔率之间的比率（开盘/收盘）。知道“真实”结果概率（50%）后，我们可以计算出所有10,000场比赛中开盘赔率和收盘赔率的预期回报。最后，我们可以绘制出开盘和收盘赔率的预期回报随着开盘/收盘赔率之比的变化而变化的情况，正如我之前对平博的比赛赔率所做的一样。

下方六张图表中的第一张为模型结果。蓝线和红线表示在开盘/收盘赔率-1（x轴）上投下10,000个投注之后，50场比赛中固定金额投注（y轴）在开盘赔率和收盘赔率上分别获得的平均预期利润回报。看起来不太像上文中的平博数据。

尽管总体来看我的开盘和收盘赔率在理论上都有效，因为它们平均而言都与“真实”价格相吻合，但事实上开盘/收盘赔率之比仅仅预测了一半的预期利润（OCRYCOP = 0.5）。例如，110%的比率会在开盘赔率上给出105%的回报（或者5%的利润收益），而在收盘赔率上给出95%的回报（或者5%的营业损失）。 

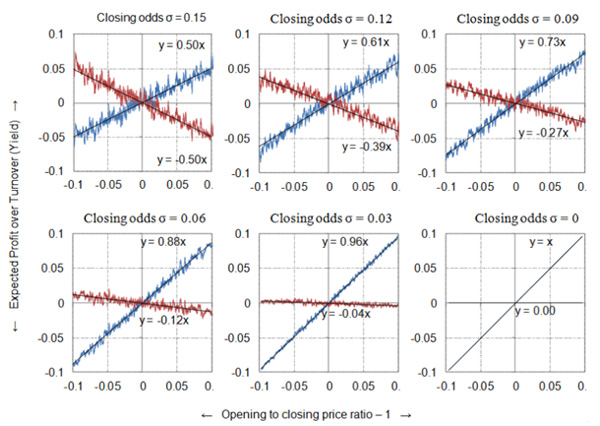
显然，在这个情况中，我们的开盘/收盘赔率之比并不能很好地预测利润率，由此可推出，我们的收盘赔率单独来看并不是非常有效。理由当然很简单。首先，我们知道我们的收盘赔率单独来看并不太有效——他们并不都和“真实”赔率2.00一样，因为我故意让它们在那个数字左右随机变化。

其次，当我的随机赔率生成器输出高开盘赔率和低收盘赔率时，就会出现最大的开盘/收盘赔率之比。这里生成的最大比率是1.55（开盘赔率2.27，收盘赔率1.46）。实际上，当“真实”价格为2.00时，我们的预期利润在2.27的开盘赔率上为2.27/2.00 - 1 = 0.135或13.5%，而不是我最初假设预测的55%。

上方另外五张图表重复了我的模型，但是逐渐降低我的收盘赔率中的随机变动性（标准差），每次减量为0.03（同时在开盘赔率中保持相同的变动性）。你会注意到，随着2.00“真实”价格的收盘赔率变动性的减小，OCRYCOP值越来越趋近1。在所有收盘赔率都为2.00（因此每个赔率单独来看都百分百有效）的极端情况中，相关性是完美的1：1。

再看看之前那张平博真实投注赔率的图表。趋势线（以及它们的方程式）非常吻合我们的模型示例，显示出完美的相关性。然而，我们可以清楚地看到仍然存在潜在的变动性——圆点并不都完美地落在趋势线上。其中某些显然是因为运气对真实世界的实际结果产生了影响（因为我的模型使用的是预期利润，消除了好运和坏运的影响）。 

虽说如此，相信每个收盘赔率都完美吻合“真实”赔率显然是完全不现实的。然而问题在于，如果没有完全有效的单个收盘赔率，我们就不得不接受开盘/收盘赔率之比与预期回报之间不太完美的相关性（OCRYCOP < 1）。那么有没有办法解决它呢？我将在本文的第二部分给出答案。