梅克尔树（Merkle trees）是区块链的基本组成部分。虽说从理论上来讲，没有梅克尔树的区块链当然也是可能的，你只需创建直接包含每一笔交易的巨大区块头（block header）就可以实现，但这样做无疑会带来可扩展性方面的挑战，从长远发展来看，可能最后将只有那些最强大的计算机，才可以运行这些无需受信的区块链。 正是因为有了梅克尔树，以太坊节点才可以建立运行在所有的计算机、笔记本、智能手机，甚至是那些由Slock.it生产的物联网设备之上。那么，究竟梅克尔树是如何工作的呢，它们又能够提供些什么价值呢，现在以及未来的？

梅克尔树的基础知识

首先，咱们先来讲点基础知识。梅克尔树，一般意义上来讲，它是哈希大量聚集数据“块”（chunk）的一种方式，它依赖于将这些数据“块”分裂成较小单位（bucket）的数据块，每一个bucket块仅包含几个数据“块”，然后取每个bucket单位数据块再次进行哈希，重复同样的过程，直至剩余的哈希总数仅变为1:即根哈希（root hash）。

梅克尔树最为常见和最简单的形式，是二叉梅克尔树（ binary Mekle tree），其中一bucket单位的数据块总是包含了两个相邻的块或哈希，它的描述如下：

graph TD A[6c0a] --> B[5c71] A --> C[8f74] B --> D[ec20] B --> E[781a] C --> F[3b95] C --> G[0d16] D --> H[bq3w:5] D --> I[CX7j:27] E --> J[1FXq:18] E --> K[9Dog:64] F --> L[zUfe:30] F --> M[jx5R:2] G --> N[yo3G:43] G --> O[vcc1:48]

那么，这种奇怪的哈希算法有什么好处么？为什么不直接将这些数据块串接成一个单独的大块，用常规的哈希算法进行呢？答案在于，它允许了一个整齐的机制，我们称之为梅克尔证明（Merkle proofs）：

graph TB A[6c0a] --> B[5c71] A --> C[8f74] B --> D[ec20] B --> E[781a] C --> F[3b95] C --> G[0d16] D --> H[bq3w:5] D --> I[CX7j:27] E --> J[1FXq:18] E --> K[9Dog:64] F --> L[zUfe:30] F --> M[jx5R:2] G --> N[yo3G:43] G --> O[vcc1:48] style A fill:#f9f style B fill:#f9f style E fill:#f9f style C fill:#83fcea style D fill:#83fcea style J fill:#83fcea style F fill:#ff7a28 style G fill:#ff7a28 style H fill:#ff7a28 style I fill:#ff7a28 style L fill:#ff7a28 style M fill:#ff7a28 style N fill:#ff7a28 style O fill:#ff7a28 style K fill:#00ff00

一个梅克尔证明包含了一个数据块，这颗梅克尔树的根哈希，以及包含了所有沿数据块到根路径哈希的“分支”。有人认为，这种证明可以验证哈希的过程，至少是对分支而言。应用也很简单：假设有一个大数据库，而该数据库的全部内容都存储在梅克尔树中，并且这颗梅克尔树的根是公开并且可信的（例如，它是由足够多个受信方进行数字签名过的，或者它有很多的工作量证明）。那么，假如一位用户想在数据库中进行一次键值查找（比如：“请告诉我，位置在85273的对象”），那他就可以询问梅克尔证明，并接受到一个正确的验证证明，他收到的值，实际上是数据库在85273位置的特定根。它允许了一种机制，既可以验证少量的数据，例如一个哈希，也可以验证大型的数据库（可能扩至无限）。

比特币系统的梅克尔证明

梅克尔证明的原始应用是比特币系统（Bitcoin），它是由中本聪（Satoshi Nakamoto）在2009年描述并且创造的。比特币区块链使用了梅克尔证明，为的是将交易存储在每一个区块中：

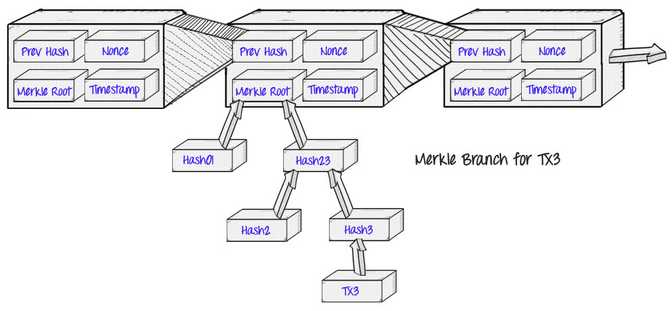
而这样做的好处，也就是中本聪描述到的“简化支付验证”（SPV）的概念:而不是下载每一笔交易以及每一个区块，一个“轻客户端”（light client）可以仅下载链的区块头，每个区块中仅包含五项内容，数据块大小为80字节：

1. 上一区块头的哈希值
2. 时间戳
3. 挖矿难度值
4. 工作量证明随机数（nonce）
5. 包含该区块交易的梅克尔树的根哈希

如果一个轻客户端希望确定一笔交易的状态，它可以简单地要求一个梅克尔证明，显示出一个在梅克尔树特定的交易，其根是在主链（main chain，非分叉链）上的区块头。

它会让我们走得很远，但比特币的轻客户确实有其局限性。一个特别的限制是，它们虽然可以证明包含的交易，但无法证明任何当前的状态（例如：数字资产的持有，名称注册，金融合约的状态等）。你现在拥有了多少个比特币？一个比特币轻客户端，可以使用一种协议，它涉及查询多个节点，并相信其中至少会有一个节点会通知你，关于你的地址中任何特定的交易支出，而这可以让你实现更多的应用。但对于其他更为复杂的应用而言，这些远远是不够的。一笔交易影响的确切性质（precise nature），可以取决于此前的几笔交易，而这些交易本身则依赖于更为前面的交易，所以最终你可以验证整个链上的每一笔交易。为了解决这个问题，以太坊的梅克尔树的概念，会更进一步。

以太坊的梅克尔证明

以太坊的每一个区块头，并非只包含一颗梅克尔树，而是包含了三颗梅克尔树，分别对应了三种对象：

1. 交易（Transactions）
2. 收据（Receipts，基本上，它是展示每一笔交易影响的数据条）
3. 状态（State）

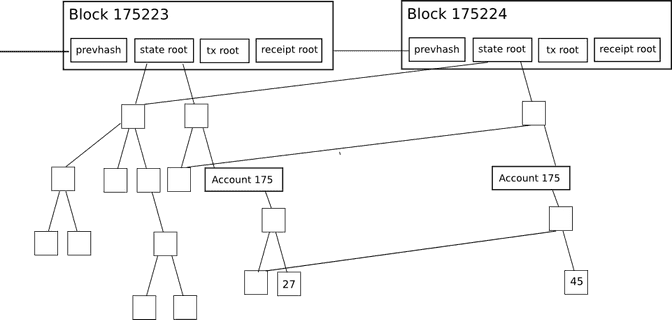
这使得一个非常先进的轻客户端协议成为了可能，它允许轻客户端轻松地进行并核实以下类型的查询答案：

1. 这笔交易被包含在特定的区块中了么？
2. 告诉我这个地址在过去30天中，发出X类型事件的所有实例（例如，一个众筹合约完成了它的目标）
3. 目前我的账户余额是多少？
4. 这个账户是否存在？
5. 假装在这个合约中运行这笔交易，它的输出会是什么？

第一种是由交易树（transaction tree）来处理的；第三和第四种则是由状态树（state tree）负责处理，第二种则由收据树（receipt tree）处理。计算前四个查询任务是相当简单的。服务器简单地找到对象，获取梅克尔分支，并通过分支来回复轻客户端。

第五种查询任务同样也是由状态树处理，但它的计算方式会比较复杂。这里，我们需要构建下我们称之为梅克尔状态转变的证明（Merkle state transition proof）。从本质上来讲，这样的证明也就是在说“如果你在根S的状态树上运行交易T，其结果状态树将是根为S'，log为L，输出为O” （“输出”作为存在于以太坊的一种概念，因为每一笔交易都是一个函数调用，它在理论上并不是必要的）。

为了推断这个证明，服务器在本地创建了一个假的区块，将状态设为 S，并假装是一个轻客户端，同时请求这笔交易。也就是说，如果请求这笔交易的过程，需要客户端确定一个账户的余额，这个轻客户端会发出一个余额疑问。如果这个轻客户端需要检查存储在一个特定合约的特定项目，该轻客户端会对此发出针对查询。服务器会正确地“回应”它所有的查询，但服务器也会跟踪它所有发回的数据。然后，服务器会把综合数据发送给客户端。客户端会进行相同的步骤，但会使用它的数据库所提供的证明。如果它的结果和服务器要求的是相同的，那客户端就接受证明。

帕特里夏树（Patricia Trees）

前面我们提到，最为简单的一种梅克尔树是二叉梅克尔树。然而，以太坊所使用的梅克尔树则更为复杂，我们称之为“梅克尔.帕特里夏树”（Merkle Patricia tree），这在我们的文档中有提到过。本文不会详细说明它的概念。如果你想了解的话，可以在这篇和这篇文章中找到答案，本文中，我仅仅会讨论下基本的论证。

二叉梅克尔树对于验证“清单”格式的信息而言，它是非常好的数据结构，本质上来讲，它就是一系列前后相连的数据块。而对于交易树来说，它们也同样是不错的，因为一旦树已经建立，花多少时间来编辑这颗树并不重要，树一旦建立了，它就会永远存在。

而对状态树来说，情况会更复杂些。以太坊中的状态树基本上包含了一个键值映射，其中的键是地址还有各种值，包括账户的声明、余额、随机数、代码以及每一个账户的存储（其中存储本身就是一颗树）。例如，摩登测试网络（the Morden testnet ）的创始状态如下所示：

{
  "0000000000000000000000000000000000000001": { "balance": "1" },
  "0000000000000000000000000000000000000002": { "balance": "1" },
  "0000000000000000000000000000000000000003": { "balance": "1" },
  "0000000000000000000000000000000000000004": { "balance": "1" },
  "102e61f5d8f9bc71d0ad4a084df4e65e05ce0e1c": {
    "balance": "1606938044258990275541962092341162602522202993782792835301376"
  }
}

然而，不同于交易历史记录，状态树需要经常地进行更新：账户余额和账户的随机数nonce经常会更变，更重要的是，新的账户会频繁地插入，存储的键（ key）也会经常被插入以及删除。而这样的数据结构设计，我们可以在一次插入、更新编辑或者删除操作之后，快速地计算出新的树根（tree root），而无需重新计算整颗树。此外，它还有两个灰常好的次要特性：

1. 树的深度是有限制的，即使考虑攻击者会故意地制造一些交易，使得这颗树尽可能地深。不然，攻击者可以通过操纵树的深度，执行拒绝服务攻击（DOS attack），使得更新变得极其缓慢。
2. 树的根只取决于数据，和其中的更新顺序无关。换个顺序进行更新，甚至重新从头计算树，并不会改变根。

而帕特里夏树，简单地说，或许最接近的解释是，我们可以同时实现所有的这些特性。其工作原理，最为简单的解释是，一个以编码形式存储到记录树的“路径”的值。每个节点会有16个子（children），所以路径是由十六进制编码来确定的：例如，狗（dog）的键的编码为 6 4 6 15 6 7，所以你会从这个根开始，下降到第六个子，然后到第四个，并依次类推，直到你达到终点。在实践中，当树稀少时也会有一些额外的优化，我们会使过程更为有效，但这是基本的原则。